APC Houses
Contents
Construction
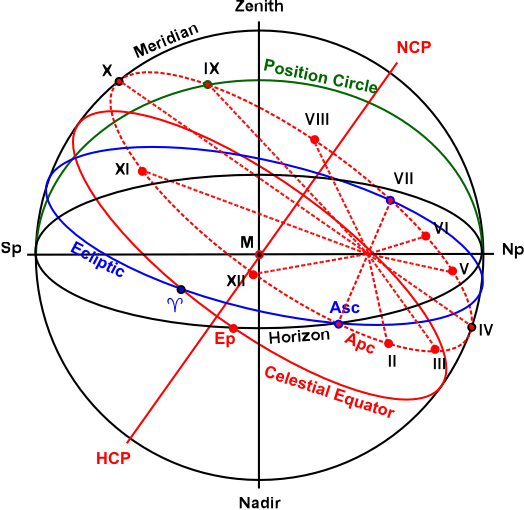
1. WvA astrologers use house cusps defined by the intersections of ten planes of oblique ascension with the ecliptic plane. First the Ascendant Parallel Circle (APC) is constructed, a plane through the ascendant point, perpendicular to the celestial equator. In the diagram the APC is represented as the red elliptic dotted line.
2. The APC is then divided in six equal parts under, and six equal parts above the horizon. The division is represented in the diagram by red dotted lines, with numbers of cusps in black next to the division points.
3. Through the division points of the sixfold division six planes of oblique ascension are constructed. (position circle, green line) Only one of these planes is drawn in the diagram. Two of these planes are the horizon (black) and the meridian (black) planes. These planes define the ascendant, descendant, MC and IC. The intersections of the other planes (green) with the ecliptic (blue) define the other cusps.
The APC house system was developed by L. Knegt, and has been applied within the Werkgemeenschap van Astrologen (WvA) in the Netherlands since its establishment in 1947. The WvA is also known as the "Ram School".
Formulas
C-code
<TEXTAREA id='code' cols=68 rows=75> /*
APC.C
APC table of houses, including the values of labda-z and beta-z
Written in Microsoft C by Ingmar de Boer
Checked: 12 May 2002
- /
- include <stdio.h>
- include <math.h>
/* Utility functions and global variables */ double pi = 3.141592653589792907377; double rad(double gr) {return pi * gr / 180.0;} double gra(double ra) {if (ra<0) ra=ra+2*pi; return fmod((180.0 * ra / pi), 360.0);}
/* Labda-z (input ph, e, az in radians, output in degrees) */ double labdaz(double ph, double e, double az) {
return gra(atan2(sin(az) * cos(e) * tan(ph) - sin(e),
cos(az) * tan(ph)));
}
/* Beta-z (input ph, e, az in radians, output in degrees) */ double betaz(double ph, double e, double az) {
return asin(-cos(ph) * cos(e) - sin(ph) * sin(e) * sin(az)) * 180.0 / pi;
}
/* A.P.C. houses (input ph, e, az in radians, output in degrees) */ double sector(int n, double ph, double e, double az) {
double dasc, kv, a;
kv = atan(tan(ph) * tan(e) * cos(az)/(1 + tan(ph) * tan(e) * sin(az))); dasc = atan(sin(kv) / tan(ph));
if (n<8) a = kv + az + pi/2 + (n - 1) * (pi/2 - kv) / 3; else a = kv + az + pi/2 + (n - 13) * (pi/2 + kv) / 3;
return gra(atan2(tan(dasc) * tan(ph) * sin(az) + sin(a),
cos(e) * (tan(dasc) * tan(ph) * cos(az) + cos(a)) + sin(e) * tan(ph) * sin(az - a)));
}
int main() {
int n; double e=23.43929111; /* e for epoch 2000,0 */ double ph; double az;
for (ph=0;ph<90;ph++)
for (az=0;az<=360;az+=5)
printf("%2.0f, %03.0f, %03.2f, %02.2f, %03.2f, %03.2f, %03.2f, %03.2f,
%03.2f, %03.2f, %03.2f, %03.2f, %03.2f, %03.2f, %03.2f, %03.2f\n",
ph, az,
labdaz(rad(ph), rad(e), rad(az)), betaz(rad(ph), rad(e), rad(az)),
sector(10, rad(ph), rad(e), rad(az)),
sector(11, rad(ph), rad(e), rad(az)),
sector(12, rad(ph), rad(e), rad(az)),
sector( 1, rad(ph), rad(e), rad(az)),
sector( 2, rad(ph), rad(e), rad(az)),
sector( 3, rad(ph), rad(e), rad(az)),
sector( 4, rad(ph), rad(e), rad(az)),
sector( 5, rad(ph), rad(e), rad(az)),
sector( 6, rad(ph), rad(e), rad(az)),
sector( 7, rad(ph), rad(e), rad(az)),
sector( 8, rad(ph), rad(e), rad(az)),
sector( 9, rad(ph), rad(e), rad(az))
);
return 0;
}; </TEXTAREA>
More
- Here is a Javascript form for APC-houses.
- View the website of the Werkgemeenschap van Astrologen.
- The Table of Houses for the APC system, which I have made for the WvA.