Authorship Attribution Method
A Statistical Authorship Attribution Method Applied to the Buddhist Scriptures of Asaṅga and Maitreya
Introduction
Studying what has been written on the scriptures attributed to Asaṅga and Maitreya, one is easily tempted to speculate on using a statistical method to compare these texts stylistically. Reading some articles of the last decade on the subject of statistical authorship attribution methods, I have learnt that there are indeed methods that can be used fruitfully to decide between different possible authors for a text. Common N-Gram analysis (CNG), one of the most successful of these, has been applied experimentally also to texts written in non-Western languages. We could try to apply this method on the available digitalised texts of Asaṅga and Maitreya, and see if the results might point in one particular direction within the rather large variety of theories concerning the authorship of these scriptures.
The Data Set and Preprocessing
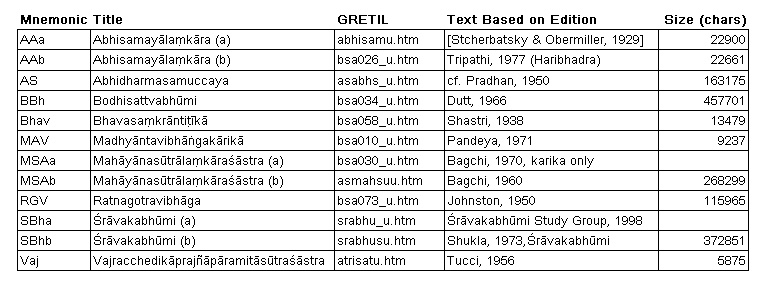
In researching authorship using statistical methods, we need texts in their original languages, as the translation process introduces too much bias to identify the author’s style of writing. Many Sanskrit Buddhist texts have been digitalised in the last decade, among which are quite a number of the scriptures attributed to Asaṅga. A source for these digitalised texts is the GRETIL archive, the “Göttingen Register of Electronic Texts in Indian Languages”, which is found on the World Wide Web at The Unicode (UTF-8) encoded versions of the texts are the ones we need here. The available texts are summed up in Table 1 below
Table 1
Before applying CNG, the texts should be preprocessed by what is called canonicising, that is removing all “unhistorical” elements, like titles or verse numbers. Canonicising could also involve unifying case, stripping punctuation, stripping numbers and normalising spaces. The text size in Table 1 is the size in UTF-8 characters after canonicising. Some experimenting with the raw GRETIL files shows that preprocessing is indeed necessary in order to obtain reliable results. The beginning of a preprocessed text as used in this article looks like
Not for all digitalised texts the canonicising is straightforward, because some are in pausa (without external sandhi). In some Sanskrit texts, missing lines are suppleted by lines in Tibetan. Having put these texts aside for convenience, this leaves us with 10 out of a total of 12 digitalised texts.
The Training Set
One or more texts are chosen as a training set, serving as a reference for the quantification of differences between the texts. Most suitable as a training text would be those for which the author is known beyond doubt, or (in our case) least doubtful.
They should be written by only one author, they should not be Indian style (sub-) commentaries, and they should be large enough (number of characters) to produce distinctive results. If possible they should have some variety, in terms of their subjects.
Unfortunately we have in our collection of digitalised texts only a few examples where the author is more or less undisputed. The most important of which will be the MAV, which is commonly attributed to Maitreya or Maitreyanātha. The MAV is not a commentary, which is positive, but it is not a very long text. On the other hand the AS is invariably attributed to Asaṅga himself. It is a bit longer than the MAV. For Asaṅga as an author, the best training text will therefore be the AS.
Moreover, for our purpose here Maitreya and Maitreyanātha can be considered the same person, or entity. We will therefore use the name Maitreyanātha from now on for this person or entity, as this seems to be most accurate.
Event Frequencies
The most reliable authorship attribution methods seem to be those based on n-grams, like CNG. Many of the methods available are only suitable for texts in Western languages, or only for the English language. CNG does not have this restriction. In this method, all sequences of n characters are generated from the text, or preferably a set of texts, and their frequences counted. The list of n-grams with their frequencies constitute a more or less reliable author profile (histogram), which is then compared to other profiles. A profile of 6-grams with their absolute frequencies can be represented like
The profile is cut off at a certain limit (culling), leaving only the most relevant (e.g. most frequent) events. Then a procedure is applied to compare the profile generated from the training text with the other profiles, of the texts of which the author is unknown. One of the ways of comparing is calculating distances between the profiles, and evaluating these.
Vlado Kešelj (2003) “revived” the use of n-grams for authorship attribution, by an earlier study. In his article on n-grams, Kešelj uses a simple procedure to calculate a distance between two profiles. Besides English and Middle English texts, trials were done with Greek and Chinese, for which the results were only slightly less accurate than for the English texts. In a later trial this approach proved to be successful (Juola 2008).
Some of the more succesful using CNG employ part-of-speech-tagging (POS) or which an automated Sanskrit POS-tagger is needed. Such POS-taggers for Sanskrit are becoming avaiblable in the past few years, but as it is they are not easily adaptable for use in this particular investigation. Methods using word counts are not suitable, word separation not have been applied consistently in the ancient Sanskrit manuscripts. Therefore in our case, that is dealing with Sanskrit texts, the best way to go is using a method employing n-grams based on simple character n-grams.
Calculating Distance
I have prepared a PHP (see appendix) for generating two profiles from two UTF-8 encoded texts and calculating their distance following the description of Kešelj (2004). I have adjusted the distance calculation so, that whenever an n-gram is present in only one of the profiles, no distance term is added. This provides a numerically different, but slightly more realistic result. The formula for distance is basically unchanged
Σ (2 . () - )) / () +
∈ D ∩ D
In tis formula, x is an n-gram in profiles D and D, and ) and ) their respective relative frequencies, that is absolute frequencies divided by the total n-gram count.
In Kešelj’s trials, the results with n-grams are most accurate when the number n is around 6. For n<=2 the results are unreliable. For our purpose we will calculate the distances to a training text profile for 3 <= n <= 8. The most succesful limit (L) for culling proves to be around 2000 n-grams, so we will also follow Kešelj there.
The distances calculated are summed up in Table 2.
Table 2
Evaluating Clustering
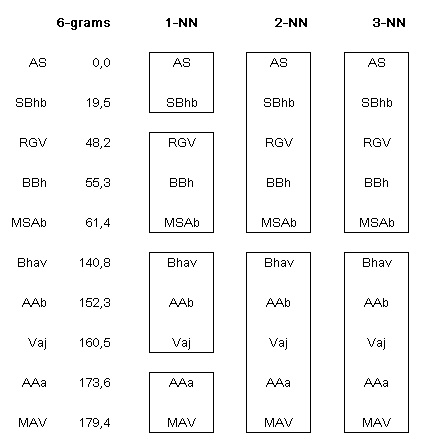
To categorize the texts according to their distance to the training text, we will make use of the k-NN algorithm. In the k-NN algorithm, for example for k=2 we connect every element with its two nearest neighbours. In Table 3 we can see that k-NN with k=2 and k=3 results in a consistent structure of two clusters. This is the case for all n we investigated. For k=1 the groups differ with different n. For k>3 all texts are in the same group.

Table 3
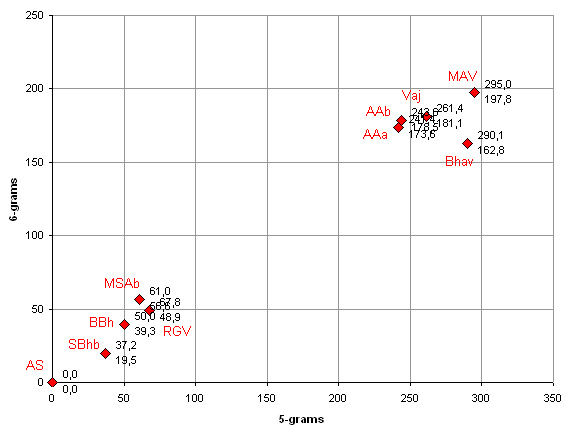
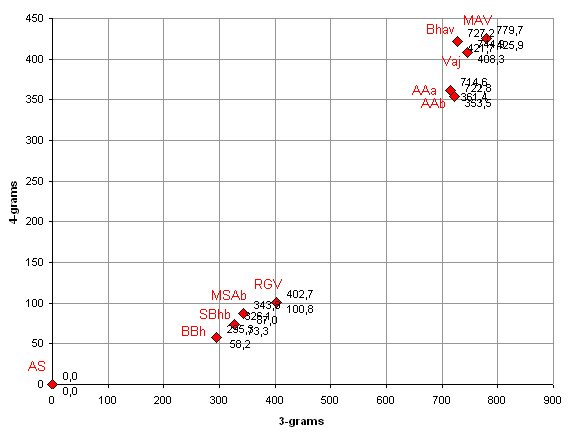
We can set up some 2D graphs visualising the distances, for 5- and 6-grams, 3- and 4-grams, and 7- and 8-grams, see the Figures 1-3 respectively.
Figure 1

Figure
2
Figure 3
Interpretation and Observations
In Figure 1 we see two clearly distinguished clusters, one being closer to the AS, and the other to the MAV, which we will call clusters 1 and 2 respectively. In Figure 2 we see the same groups, keeping in mind that 3- and 4-grams (and 7- and 8-grams) would be less accurate than 5- and 6-grams. In Figure 3 again we see the same clusters, with cluster 1 more spread out across the diagonal axis.
We might interpret cluster 1 as the Maitreyanātha cluster, as it contains the MAV, and most of the texts in cluster 1 are most often attributed to Maitreyanātha, and cluster 2 as the Asaṅga cluster, containing the AS, YBh and other texts most often attributed to Asaṅga.
Results are summarized in Table 4, together with some of the traditions and modern views concerning the authorship of the scriptures under consideration. (without aspiration to completeness) Wherever a traditional or theoretical view does not correspond to the cluster separation we found here, the indicator is set in red.

Table 4
Finally, we might sum up some observations.
Theories supported by our findings are those of Lévi (100%), Ui (75%), followed by Huì Lì, mKhas Grub and Bu sTon (all 67%). A theory unsupported is Winternitz’ (75%).
The Chinese and Tibetan traditions both correspond quite closely (71% and 67%) to the cluster separation we found. However in the Chinese tradition, the Vaj and the YBh are attributed to Asaṅga while they are part of our Maitreyanātha cluster. In the Tibetan tradition, the MSA and the RGV are attributed to Maitreyanātha while they are part of our Asaṅga cluster.
The fact that the two clusters are so clearly distinguished, suggests that there will be differences in vocabulary, style, background, which might be demonstrated using other, more direct methods. CNG, like any other authorship attribution method, does not by itself compare author specific traits.
The method can therefore also be used to compare genre, style, consistency, etc. The way we used it here, it is not possible to determine that the texts in one cluster are by the same author. Crucial is that we have only one text (AS) of which the author is undisputed.
In Figure 1, the MSA and the RGV are closest to each other, almost as close as the two versions of the AA, our AAa and AAb, which are textually almost identical, however this must be coincidental, as in Figures 2 and 3 they are much further apart. Also the outlaying position of the Bhav in Figure 3 is coincidental.
Interestingly, all texts in which Maitreyanātha is explicitly stated as an author in a heading or closing formula, are part of the Maitreyanātha cluster. (AAa kṛtirmaitreyanāthasya; AAb āryamaitreyanāthaviracitam; Bhav maitreyanāthakṛtā, paṇḍitamaitreyanāthakṛtaḥ; MAV āryamaitreyapraṇītā) The Vaj’s closing formula “kṛtir iyam āryāsaṅgapādānām iti” may point to the Chinese tradition. Nevertheless the Vaj is part of our Maitreyanātha cluster.
The discussion whether Maitreyanātha is a mythological or historical figure is perhaps ant here to the extent to which a mythological character can or cannot be considered the author of a text. Ttha’s description of the process of inspired writing suggests that Maitreya dictated the texts to Asaga, memorizing them literally, and not for many years later entrusted them to the palmleaf. This way, Maitreya’s style of writing could be different from Asaga’s in an way than when Maitreya (-nātha) would be a human author. Otherwise we will not be able to distinguish between the styles of Maitreyanātha and Asaṅga. Vice versa, if we conclude from the separation of the two clusters, that there are two different authors here, either we believe in a process of inspired writing as in Ttha’s description, or we see Maitreyanātha as a human author.
The SBh and BBh containing most “śrāvakayānist elements” are part of the Asaṅga cluster. They are closest to the AS, which is also in many aspects a śrāvakayāna-style work. The SBh and BBh correspond to each other very closely, as might be expected, both being part of the larger YBh.
Kešelj, V., and others, N-gram-based author profiles for authorship attribution, in Proceedings of the Conference of the Pacific Association for Computational Linguistics, PACLING’03, pp. 255-264, Halifax, 2003
Juola, P., Authorship Attribution, in Foundations and Trends in Information Retrieval (R), Vol. 1, No. 3 (2006), pp. 233-334, [Pittsburg], 2008
Kešelj, V., and Cercone, N., CNG Method of Weighted Voting, in Ad-hoc Authorship Attribution Competition, Halifax, 2004
Appendix: PHP5 code
// Program: ngrams6_.php
// Date: 23 januari 2013
// Language: PHP 5.x
function generate($str, $l) {
$ret = array();
if ($l > 0) {
$len = mb_strlen($str, "UTF-8");
for ($i = 0; $i < $len; $i++) {
$h = mb_substr($str, $i, $l, "UTF-8");
if (mb_strlen($h, "UTF-8")==$l) {
$ret[] = $h;
return $ret;
function distance_($f1, $f2, $cnt1, $cnt2) {
if (isset($f1) && isset($f2)) {
$f2 = $f2 / $cnt2;
$f1 = $f1 / $cnt1;
$f2 = 2 * ($f1 - $f2) / ($f1 + $f2);
$f2 = $f2 * $f2;
else {
$f2 = 0; // 4 acc. to Keselj
return $f2;
function distance($arr1, $arr2, $cnt1, $cnt2) {
$arr3 = array_fill_keys(array_keys($arr1), "");
$arr4 = array_fill_keys(array_keys($arr2), "");
$arr = array_merge($arr3, $arr4);
foreach ($arr as $key => $value) {
$arr[$key] = distance_($arr1[$key], $arr2[$key], $cnt1, $cnt2);
arsort($arr, SORT_NUMERIC);
return $arr;
function profile(&$text, $n, $limit, &$cntall, $name) {
// preprocess
$text0 = str_replace("\'", "$", $text);
$len = mb_strlen($text0, "UTF-8");
// generate all n-grams
$arr = generate($text0, $n);
// create profile
$arr = array_count_values($arr); // generate absolute frequencies
arsort($arr, SORT_NUMERIC); // reverse sort by frequency
$cntuniq = count($arr); // number of unique generated n-grams
$cntall = array_sum($arr); // number of all generated n-grams
$arr = array_slice($arr , 0, $limit, true); // culling